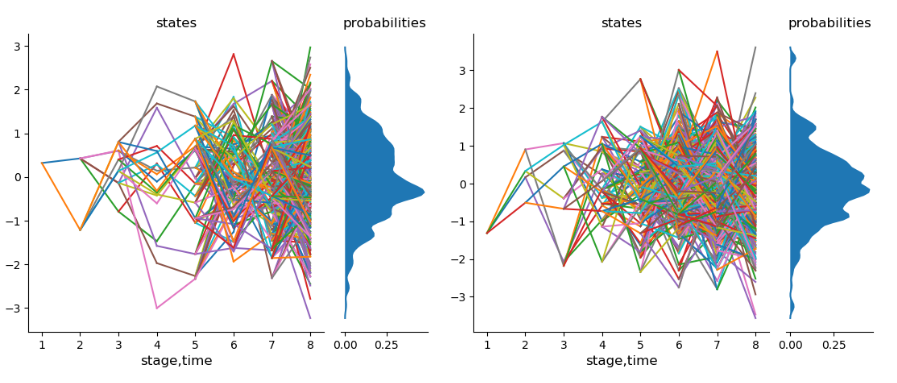
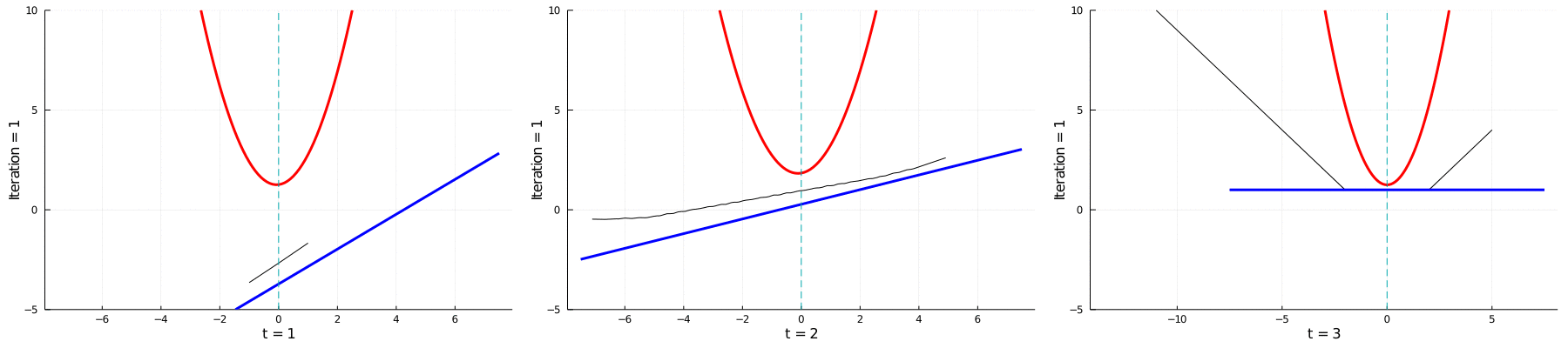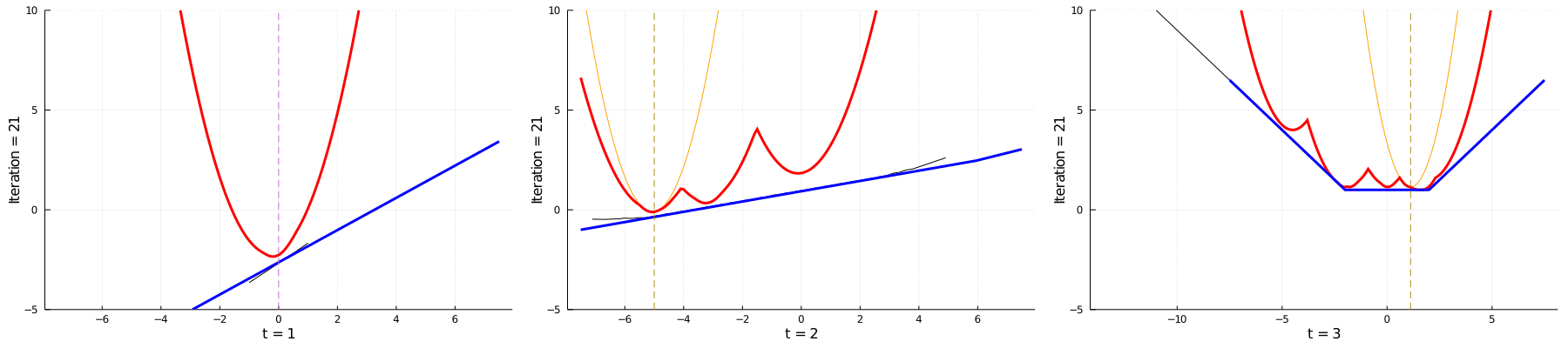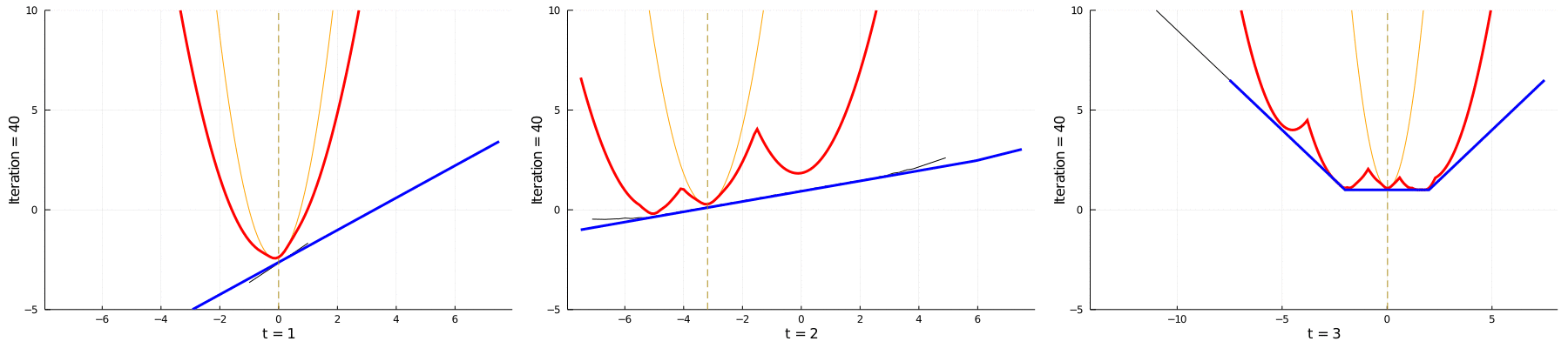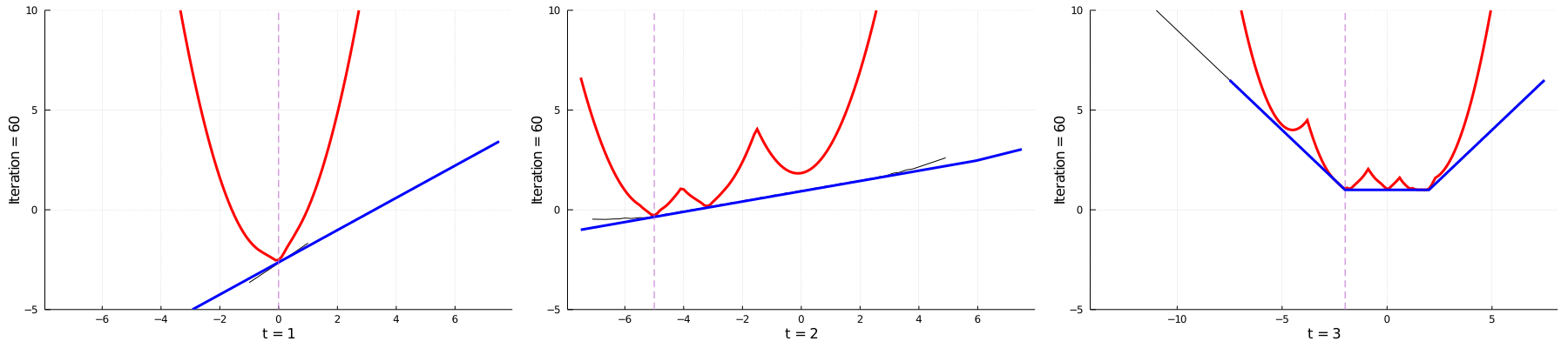
Currently, I am a postdoc at FGV EMAp in Brazil, under the supervision of Vincent Guigues.
I was a PhD student in optimization from September 2017 to December 2020 at the CERMICS, École des Ponts ParisTech and the CMAP, École Polytechnique under the supervision of Jean-Philippe Chancelier and Marianne Akian.
I graduated in Mathematics from Paris-Saclay University, formely known as Paris-Sud University (Orsay).
Last update: May 2022.
Stochastic Optimal Control ; Stochastic Programming ; SDDP ; Tropical Algebra
The dynamic programming approach applied to stochastic control problems allows one to find optimal feedback policies but it requires solving a nonlinear equation or a fully nonlinear partial differential equation of Hamilton-Jacobi type over the state space. Hence, this method suffers from the curse of dimensionality, for instance grid-based methods like finite-difference or finite element methods have a complexity exponential in the dimension of the state space.
Several methods were created to bypass this difficulty by assuming some structure on the problem. Examples are the max-plus based method of McEneaney and the Stochastic Dual Dynamic Programming (SDDP) algorithm of Pereira and Pinto.
We associate and compare these methods in order to solve more general structures, in discrete time.I defended my Ph.D. in 2020, the thesis document can be found here (the introduction is in French, then translated in English and the remainder is in English as well).
With Zheng Qu, 10 pages. We introduce an entropic regularization of the Nested Distance between scenario trees (i.e. stochastic processes which are discrete and finite both in time and space). It is a simple adaptation of Sinkhorn's algorithm for discrete Optimal Transport to this case. We present some numerical examples.
With Jean-Philippe Chancelier and Michel De Lara, 32 pages. We give a general necessary and sufficient condition on the interchange between integration and minimization. We recover (and slightly extend) some classical results of the litterature.
With Marianne Akian and Jean-Philippe Chancelier, 23 pages, 3 figures. We approximate the Bellman value functions of a MSP by max-plus linear and min-plus linear combinations of basic functions. We give a convergence result inspired by Baucke and al. convergence result for a variant of SDDP. Illustrations in the linear-polyhedral framework.
With Marianne Akian and Jean-Philippe Chancelier, 6 pages, 3 figures. Abridged version of the one below with an emphasis on a numerical experiment.
With Marianne Akian and Jean-Philippe Chancelier, 34 pages, 7 figures. In this article, we build a common framework for both the DDP algorithm and a discrete time version of Zheng Qu's min-plus algorithm to solve deterministic multistage optimization problems. We prove its convergence under mild technical assumptions.